$\mathcal H_\infty$ and $\mathcal H_2$ norms
In modern theory control, the performances of a system can be measured with the $\mathcal H_\infty$ (H infinity) and $\mathcal H_2$ (H2) norms.
Noting $\text{Tr}()$ the trace operator, the $\mathcal H_2$ norm of a transfer matrix $\mathbf G(\mathrm s)$ between an input $\mathbf u$ and an output $\mathbf y$, such that $\mathbf y(\mathrm s) = \mathbf G(\mathrm s) \mathbf u(\mathrm s)$, is defined as:
\begin{equation}
\mid \mid \mathbf G(\mathrm s) \mid \mid_2^2 = \frac{1}{2\pi} \int_{-\infty}^{+\infty} \text{Tr}(\mathbf G^T(-j\omega) \mathbf G(j\omega)) d\omega
\end{equation}
The $\mathcal H_2$ norm can be interpreted equivalently as the output signal $\mathbf y(t)$ energy when the input signal $\mathbf u(t)$ is an impulse, or as the variance of the output signal when the input is a white noise with a unitary power spectral density. Thus, the $\mathcal H_2$ norm can for example quantify the pointing error caused by measurement noise, or the response of the system to an impulse disturbance.
The $\mathcal L_2$ norm represents the energy of a transient signal:

And the $\mathcal H_\infty$ norm is induced by the $\mathcal L_2$ norm:
\begin{equation}
\mid \mid \mathbf G(\mathrm s) \mid \mid_{\infty} = \underset{\omega}{\text{sup }} \sigma_{\text{max}} (\mathbf G(j\omega)) = \underset{\mathbf u \neq \mathbf 0}{\text{sup }} \frac{\mid \mid \mathbf y \mid \mid_2}{\mid \mid \mathbf u \mid \mid_2}
\end{equation}
Therefore, the $\mathcal H_\infty$ norm represents the maximum amplification factor of the signal energy from the input to the output, which makes it useful to assess the performance in a control problem. Equivalently, it is also the maximum singular value ($\sigma_{\mathrm{max}}$) over all frequencies.
The standard $\mathcal H_\infty$ control problem
Let us consider the closed-loop represented as the standard LFT (Linear Fractional Transformation) form in following Figure (no parametric uncertainty is considered yet).
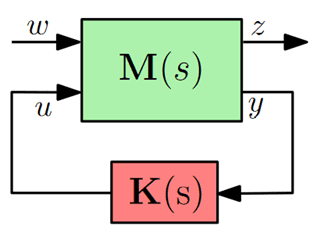
The $\mathcal H_{\infty}$ control problem consists in computing an optimal controller $\mathbf K^* (\mathrm s)$ that stabilizes the plant $\mathbf M(\mathrm s)$ and minimizes the transfer $T_{w\rightarrow z} = \mathcal F_l(\mathbf M, \mathbf K)$ (where $\mathcal F_l(.)$ denotes the lower LFT, as in Fig.~\ref{fig:standard_form}) between the exogenous input $\mathbf w$ and regulated output $\mathbf z$. The $\mathcal H_{\infty}$ control problem is stated as in [AN06c] :
\begin{equation}
\begin{array}{ll}
\underset{\mathbf K(\mathrm s) \in \mathcal K}{\text{minimize}} & \mid \mid \mathcal F_l(\mathbf M, \mathbf K) \mid \mid_{\infty} \\
\text{subject to } & \mathbf K(\mathrm s) \text{ stabilizes } \mathbf M(\mathrm s)
\end{array}
\end{equation}
where $\mathcal K$ designates the space of admissible controllers.
Solving the H infinity control problem
When $\mathcal K$ groups all full-order controllers, that is, $\mathbf K(\mathrm s)$ has the same order as the plant $\mathbf M(\mathrm s)$, the problem is convex. Several solutions to the full-order $\mathcal H_{\infty}$ problem were proposed in the 1980s and 1990s [GA94]. When the structure of the controller is imposed, the problem is non-convex, and solutions are more complex to find. Structured controllers are essential for practical applications; they include, for example: PID controllers, low-order controllers, observer-based controllers, decentralized controllers, etc.
Although the first approaches to solve the structured $\mathcal H_{\infty}$ problem were based on bilinear matrix inequalities [Apk04], they were limited to small size problems due to their complexity increasing rapidly with the number of states of the plant. On the contrary, the solution proposed in [AN06a],relying on a specific non-smooth optimization algorithm, has allowed addressing larger size problems and was implemented in Matlab with the routine systune. Contrary to the full-order problem that is convex and allows finding a global optimum, the latter approach for the structured problem only finds a locally optimal solution, which is most often satisfying but generally requires a reasonable initialization.
Multi-objectives optimization
In practical applications, it is most often necessary to simultaneously address multiple control requirements in the controller synthesis: such requirements can be to minimize the impact of an external disturbance, ensure the reference tracking with a given bandwidth, minimize of the solicitation of the actuators, or reduce the impact of the sensors noise, for example.
After augmenting the plant with weighting functions $\mathbf W_i$ translating the $N$ control requirements in the frequency domain, the multi-objectives problem can be stated as:
\begin{equation}
\begin{array}{ll}
\underset{\mathbf K(\mathrm s) \in \mathcal K}{\text{minimize}} & \mid \mid \mathbf W_1 \mathcal F_l(\mathbf M_1, \mathbf K) \mid \mid_{\infty} \\
\text{subject to } & \mid \mid \mathbf W_i \mathcal F_l(\mathbf M_i, \mathbf K) \mid \mid_{\infty} < \gamma_i\,,\, i=2,…,N \\
& \mathbf K(\mathrm s) \text{ stabilizes } \mathbf M_i(\mathrm s)\,,\, i=2,…,N
\end{array}
\end{equation}
This optimization problem, where the cost function is characterized by ($\mathbf M_1$, $\mathbf W_1$) and the i-th hard constraint is characterized by ($\mathbf M_i$, $\mathbf W_i$), is reformulated as a multidisk approach solved in [AN06b]:
\begin{equation}
\begin{array}{ll}
\underset{\mathbf K(\mathrm s) \in \mathcal K}{\text{minimize}} & \underset{i=1,…,N}{\text{max}} \alpha_i \mid \mid \mathbf W_i \mathcal F_l(\mathbf M_i, \mathbf K) \mid \mid_{\infty}
\end{array}
\end{equation}
Where the $\alpha_i$ are adjusted during optimization. Finally, let us mention that the $\mathcal H_\infty$ can be replaced by the $\mathcal H_2$ in previous equations.
H infinity robust control
Let us now consider parametric uncertainties in the system, in order to perform robust controller synthesis. Parametric uncertainties are represented by block $\Delta \in \mathbb D$, where $\mathbb D$ is the set of all possible parametric configurations, as in the classical LFT (Linear Fractional Transformation) representation:
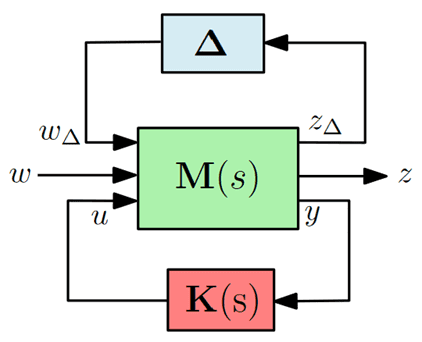
The $\mathcal H_\infty$ control problem, as defined in [ADN15], consists in computing an optimal controller $\mathbf K^* (\mathrm s) \in \mathcal K$ that minimizes the worst-case transfer:
\begin{equation}
\begin{array}{ll}
\underset{\mathbf K(\mathrm s) \in \mathcal K}{\text{minimize}} & \underset{\Delta \in \mathbb D}{\text{max}} \mid \mid \mathcal F_l(\mathcal F_u(\mathbf M, \Delta), \mathbf K) \mid \mid_{\infty} \\
\text{subject to } & \mathbf K(\mathrm s) \text{ stabilizes } \mathcal F_u(\mathbf M, \Delta) \text{ for all } \Delta \in \mathbb D
\end{array}
\end{equation}
This problem is considerably more complex. Indeed, assessing exhaustively the robustness of the closed-loop, when the controller is already given, is already an NP-hard problem.
Rather than relying on outer approximations (relaxing the problem by choosing a larger but more convenient set $\tilde{\mathbb D}$ such that $\mathbb D \subset \tilde{\mathbb D}$) like the DK-iteration method, the approach presented in [ADN15] and implemented in the systune routine of Matlab relies on inner approximations by solving the problem on a smaller subset $\mathbb D_a \subset \mathbb D$ which is computed dynamically based on a heuristic search of destabilizing configurations. This avoids the conservatism inherent to outer approximations and leads to better CPUs, but does not offer strict robustness guarantee. However, in practice, the solutions are generally acceptable and the robustness can be exhaustively verified a posteriori with $\mu$-analysis or Monte-Carlo simulations.
In practice
$\mathcal H_\infty$ / $\mathcal H_2$ synthesis is a powerful and mature tool to optimize a controller while taking into account several objectives/constraints, automatically and robustly to uncertainties, in order to reduce iterations between controller design and verification and validation (V&V) process. From the control engineer point of view, the tuning process essentially requires:
- Obtain a dynamic model of the system, possibly including parametric uncertainties under the LFT form, using for example the SDTlib.
- Formulate control requirements as the norms of adequate transfer functions between well chosen inputs andoutputs, and write weighting filters accordingly to the system’s specifications. For example, a disturbance rejection requirement can be expressed as an upper bound on the norm of the tranfer function between disturbance and pointing error, in order to ensure a specified pointing precision.
- Use the systune routine, implemented in the Robust control toolbox of Matlab.
References
[GA94] Pascal Gahinet and Pierre Apkarian. “A linear matrix inequality approach to H infinity control”. In: International Journal of Robust and Nonlinear Control 4 (1994), pp. 421–448.
[Apk04] Pierre Apkarian et al. “A spectral quadratic-SDP method with applications to fixed-order H2 and H infinity synthesis”. In: European Journal of Control 10.6 (2004), pp. 527–538.
[AN06a] Pierre Apkarian and Dominikus Noll. “Nonsmooth H infinity synthesis”. In: IEEE Transactions on Automatic Control 51.1 (2006), pp. 71–86
[AN06b] Pierre Apkarian and Dominikus Noll. “Nonsmooth optimization for multidisk H infinity synthesis”. In: European Journal of Control 12.3 (2006), pp. 229–244
[AN06c] Pierre Apkarian and Dominikus Noll. “The H infinity Control Problem is Solved”. In: Aerospace Lab 13 (2006), pp. 1–27.
[ADN15] Pierre Apkarian, Minh Ngoc Dao, and Dominikus Noll. “Parametric Robust Structured Control Design”. In: IEEE Transactions on Automatic Control 60.7 (2015), pp. 1857–1869. arXiv: 1405.4202.
