The TITOP (Two-Input Two-Output Port) approach was developed at ISAE-Supaero to model flexible structures in a multibody framework [1].
The TITOP model of a flexible body (a solar panel, for example, or an antenna, a robotic arm…) describes its dynamics independently of the rest of the system. By assembling TITOP models, we can build a model of a complex structure while retaining physical parameters for each substructure.
The following figure shows an arbitrary flexible structure denoted $L_i$, connected to a parent structure $L_i$ at point P, and to a child structure $L_{i+1}$ at point C.
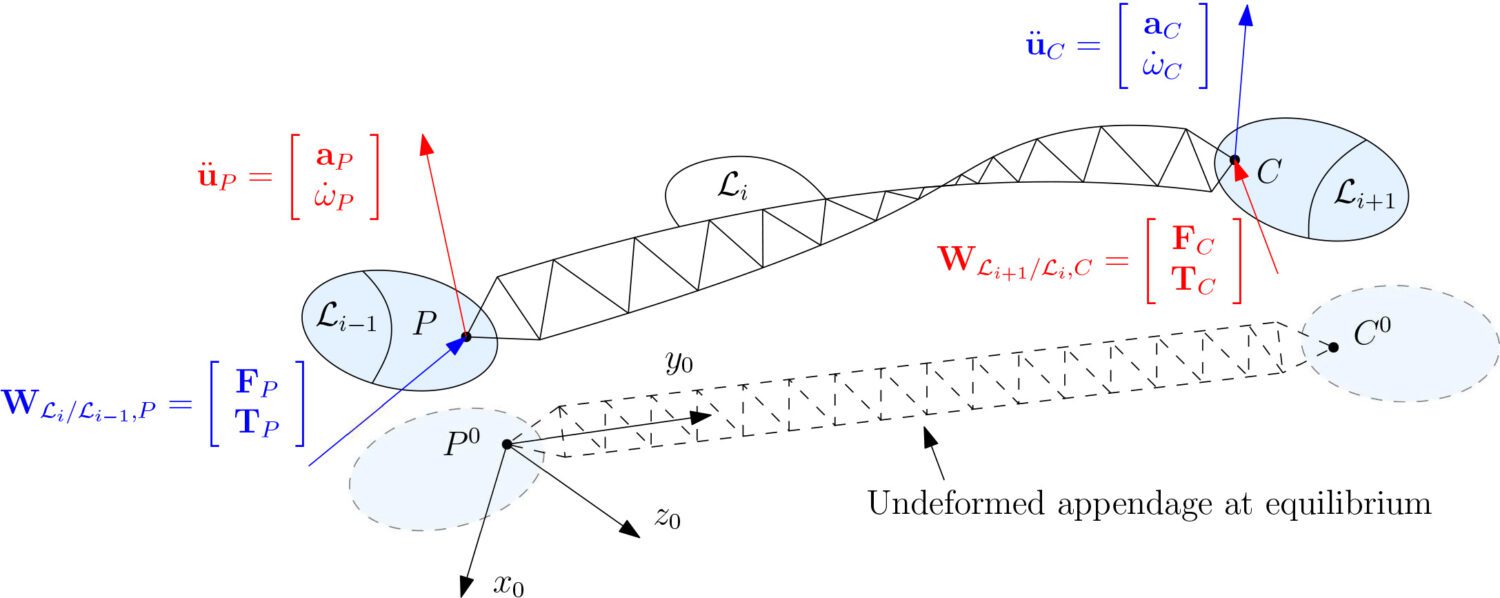
The TITOP model of this structure is the 12×12 transfer between the inputs (in red):
- $W_{L_{i+1}/L_i,P}$ the wrench torsor containing the force and torque applied by $L_{i+1}$ on $L_i$ at point C
- $\ddot u_P$ the accelerations (translation and rotations) imposed on $L_i$ at point P,
And the outputs (in blue):
- $\ddot u_C$ the resultant accelerations at point C (with rigid and flexible components),
- $W_{L_i/L_{i-1,P}}$ the wrench torsor applied by $L_i$ to $L_{i-1}$ in reaction at point P.
Here, the flexible body is clamped in P – free in C; but the SDTlib performs the necessary inversion operations to obtain any boundary conditions [2]. In addition, despite the name “TITOP”, the approach has been generalized to any number of connection points (and not just 2).
The TITOP model is built from the mechanical data of the structure. It can then be connected to the structure, both for simple configurations (such as a solar panel embedded in the central body at one point) and complex ones (open kinematic chains representing a robotic arm, plate assembly in a closed kinematic chain to model a solar panel, etc.). It is compatible with LFT (Linear Fractional Transformation) representation of uncertainties to produce a fully parameterized model.
In some cases, the model of the structure cannot be expressed independently of the rest of the structure. This is notably the case when it depends on particular equilibrium conditions, such as the presence of gravity (for a stratospheric balloon or launcher) or centrifugal force (for a spinning satellite). To express the dynaic model of the flexible body, isolated from the structure and retaining the representation of parametric uncertainties in LFT form, it is then necessary to calculate the equilibrium conditions as proposed in [3].
In SDTlib, analytical models are implemented for simple shapes (plates and beams), as well as finite element models for plate assemblies; for more complex structures, it is also possible to directly enter resonance frequencies and modal participation factors, obtained by any external software, or to directly enter the f06 file supplied by Nastran. The TITOP model is then generated, and can be used to model flexible elements of the spacecraft.
References
[1] Alazard, D., Perez, J. A., Cumer, C., & Loquen, T. (2015). Two-input two-output port model for mechanical systems. In AIAA Guidance, Navigation, and Control Conference (p. 1778).
[2] Alazard, D., Finozzi, A., & Sanfedino, F. (2023). Port inversions of parametric Two-Input Two-Output Port models of flexible substructures. Multibody System Dynamics, 57(3-4), 365-387.
[3] Kassarian, E., Sanfedino, F., Alazard, D., Chevrier, C. A., & Montel, J. (2022). Linear Fractional Transformation modeling of multibody dynamics around parameter-dependent equilibrium. IEEE Transactions on Control Systems Technology.
