Norme $\mathcal H_\infty$, norme $\mathcal H_2$
Dans la théorie moderne du contrôle, les performances de contrôle d’un système peuvent être mesurées avec les normes $\mathcal H_\infty$ (H infini) et $\mathcal H_2$ (H2).
En notant l’opérateur de trace $\text{Tr}()$, la norme $\mathcal H_2$ d’une matrice de transfert $\mathbf G(\mathrm s)$ entre une entrée $\mathbf u$ et une sortie $\mathbf y$, telle que $\mathbf y(\mathrm s) = \mathbf G(\mathrm s) \mathbf u(\mathrm s)$, est définie comme suit :
\begin{equation}
\mid \mid \mathbf G(\mathrm s) \mid \mid_2^2 = \frac{1}{2\pi} \int_{-\infty}^{+\infty} \text{Tr}(\mathbf G^T(-j\omega) \mathbf G(j\omega)) d\omega
\end{equation}
La norme $\mathcal H_2$ peut être interprétée de manière équivalente comme l’énergie du signal de sortie $\mathbf y(t)$ lorsque le signal d’entrée $\mathbf u(t)$ est une impulsion, ou la variance du signal de sortie lorsque l’entrée est un bruit blanc avec une densité spectrale de puissance unitaire. Ainsi, la norme $\mathcal H_2$ permet de quantifier l’erreur de pointage causée par le bruit de mesure, ou la réponse du système à une perturbation impulsionnelle.
La norme $\mathcal L_2$ représente l’énergie d’un signal transitoire :

Et la norme $\mathcal H_\infty$ est induite par la norme $\mathcal L_2$ :
\begin{equation}
\mid \mid \mathbf G(\mathrm s) \mid \mid_{\infty} = \underset{\omega}{\text{sup }} \sigma_{\text{max}} (\mathbf G(j\omega)) = \underset{\mathbf u \neq \mathbf 0}{\text{sup }} \frac{\mid \mid \mathbf y \mid \mid_2}{\mid \mid \mathbf u \mid \mid_2}
\end{equation}
Ainsi, la norme $\mathcal H_\infty$ représente comme le facteur d’amplification maximum de l’énergie du signal entre l’entrée et la sortie, ce qui en fait une mesure de performance pertinente pour les problèmes de contrôle. De façon équivalente, c’est la plus grande valeur singulière ($\sigma_{\mathrm{max}}$) à travers les fréquences.
Le problème standard de contrôle $\mathcal H_\infty$
Considérons la boucle fermée, représentée sous la forme LFT (Linear Fractional Transformation) standarde dans la figure suivante (aucune incertitude paramétrique n’est encore prise en compte).
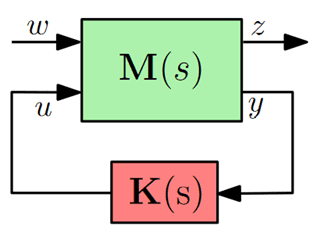
Le problème de contrôle $\mathcal H_\infty$ consiste à calculer un contrôleur optimal $\mathbf K^*(\mathrm s)$ qui stabilise le système $\mathbf M(\mathrm s)$ et minimise le transfert $T_{\mathbf w \rightarrow \mathbf z}(\mathrm s) = \mathcal F_l(\mathbf M, \mathbf K)$ (où $\mathcal F_l()$ désigne la LFT inférieure, comme dans la figure précédente) entre l’entrée exogène $\mathbf w$ et la sortie régulée $\mathbf z$. Le problème de contrôle $\mathcal H_\infty$ s’énonce comme dans [AN06c] :
\begin{equation}
\begin{array}{ll}
\underset{\mathbf K(\mathrm s) \in \mathcal K}{\text{minimiser}} & \mid \mid \mathcal F_l(\mathbf M, \mathbf K) \mid \mid_{\infty} \\
\text{tel que } & \mathbf K(\mathrm s) \text{ stabilise } \mathbf M(\mathrm s)
\end{array}
\end{equation}
où $\mathcal K$ désigne l’ensemble des contrôleurs admissibles.
Résolution du problème de contrôle H infini
Lorsque $\mathcal K$ regroupe les contrôleurs d’ordre plein, c’est-à-dire que $\mathbf K(\mathrm s)$ a le même ordre que le système $\mathbf M(\mathrm s)$, le problème est convexe. Plusieurs solutions au problème $\mathcal H_\infty$ d’ordre plein ont été proposées dans les années 1980 et 1990 [GA94]. Lorsque la structure du contrôleur est imposée, le problème est non convexe, et les solutions sont plus complexes à trouver. Les contrôleurs structurés sont essentiels pour les applications pratiques ; il s’agit, par exemple des contrôleurs PID, des contrôleurs d’ordre réduit, des contrôleurs basés sur des observateurs, des contrôleurs décentralisés, etc. Bien que les premières approches pour résoudre le problème $\mathcal H_\infty$ structuré aient été basées sur des inégalités matricielles bilinéaires [Apk04], elles étaient limitées à des problèmes de petite taille en raison de leur complexité, qui augmentait rapidement avec le nombre d’états du système. Au contraire, la solution proposée dans [AN06a], reposant sur un algorithme d’optimisation non lisse spécifiquement développé pour le contrôle $\mathcal H_\infty$, a permis de résoudre des problèmes de plus grande taille et a été implémentée dans Matlab dans la routine systune. Contrairement au problème d’ordre plein qui est convexe et qui permet de trouver un optimum global, cette dernière approche pour le problème structuré ne trouve qu’une solution localement optimale, mais cet optimum local est le plus souvent satisfaisant si le problème est bien posé.
Optimisation multi-objectifs
Dans les applications pratiques, il est généralement nécessaire d’adresser simultanément plusieurs exigences de contrôle dans la synthèse du contrôleur : ces exigences peuvent être de minimiser l’impact d’une perturbation externe, d’assurer le suivi de référence avec une bande-passante donnée, de minimiser la sollicitation des actionneurs, ou de réduire l’impact du bruit des capteurs, par exemple. Après avoir augmenté le modèle avec des filtres de pondération $\mathbf W_i$ traduisant les $N$ exigences de contrôle dans le domaine fréquentiel, le problème multi-objectifs peut être énoncé comme suit :
\begin{equation}
\begin{array}{ll}
\underset{\mathbf K(\mathrm s) \in \mathcal K}{\text{minimiser}} & \mid \mid \mathbf W_1 \mathcal F_l(\mathbf M_1, \mathbf K) \mid \mid_{\infty} \\
\text{tel que } & \mid \mid \mathbf W_i \mathcal F_l(\mathbf M_i, \mathbf K) \mid \mid_{\infty} < \gamma_i\,,\, i=2,…,N \\
& \mathbf K(\mathrm s) \text{ stabilise } \mathbf M_i(\mathrm s)\,,\, i=2,…,N
\end{array}
\end{equation}
Le problème d’optimisation, où la fonction de coût est caractérisée par $(\mathbf M_1, \mathbf W_1)$ et la i-ème contrainte, par $(\mathbf M_i, \mathbf W_i)$, est reformulé comme le problème d’optimisation multidisque [AN06b]:
\begin{equation}
\begin{array}{ll}
\underset{\mathbf K(\mathrm s) \in \mathcal K}{\text{minimiser}} & \underset{i=1,…,N}{\text{max}} \alpha_i \mid \mid \mathbf W_i \mathcal F_l(\mathbf M_i, \mathbf K) \mid \mid_{\infty}
\end{array}
\end{equation}
Où les $\alpha_i$ sont ajustés durant l’optimisation. Finalement, on peut mentionner que la norme $\mathcal H_\infty$ peut être remplacée par la norme $\mathcal H_2$ dans toutes les équations précédentes.
Contrôle H infini robuste
Ajoutons maintenant des incertitudes paramétriques au système, afin d’effectuer une synthèse robuste du contrôleur. Les incertitudes sont représentées par le bloc $\Delta \in \mathbb D$, où $\mathbb D$ est l’ensemble des configurations paramétriques possibles, selon la forme LFT (Linear Fractional Transformation) classique:
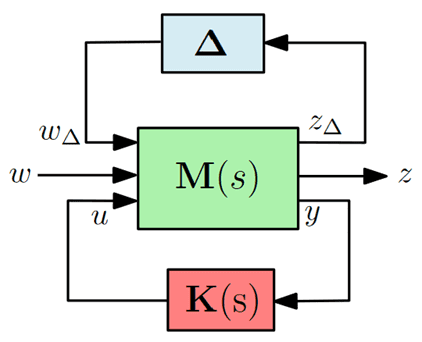
Le problème de contrôle H infini robuste, tel que formulé dans [ADN15], consiste à trouve le contrôleur optimal $\mathbf K^*(\mathrm s)$ qui minimise la norme pire-cas du transfert :
\begin{equation}
\begin{array}{ll}
\underset{\mathbf K(\mathrm s) \in \mathcal K}{\text{minimiser}} & \underset{\Delta \in \mathbb D}{\text{max}} \mid \mid \mathcal F_l(\mathcal F_u(\mathbf M, \Delta), \mathbf K) \mid \mid_{\infty} \\
\text{tel que } & \mathbf K(\mathrm s) \text{ stabilise } \mathcal F_u(\mathbf M, \Delta) \text{ pour tout } \Delta \in \mathbb D
\end{array}
\end{equation}
Ce problème est considérablement plus complexe. En effet, évaluer de manière exhaustive la robustesse de la boucle fermée, lorsque le contrôleur est déjà donné, est déjà un problème NP-difficile. Plutôt que de s’appuyer sur des approximations “externe” (simplifiant le problème en travaillant sur un ensemble plus grand $\tilde{\mathbb D}$ tel que $\tilde{\mathbb D} \in \mathbb D$) comme la méthode par itérations DK, l’approche présentée dans [ADN15] et implémentée dans la routine systune de Matlab repose sur des approximations « internes » en résolvant le problème sur un sous-ensemble plus petit $\mathbb D_a \in \mathbb D$, calculé dynamiquement sur la base d’une recherche heuristique des configurations déstabilisantes. Cela évite le conservatisme inhérent aux approximations externes et conduit à de meilleurs temps de calcul, mais n’offre pas de garantie de robustesse stricte. Cependant, dans la pratique, les solutions sont généralement acceptables et la robustesse peut être vérifiée de manière exhaustive a posteriori avec la μ-analyse ou par des simulations de Monte-Carlo.
En pratique
La synthèse $\mathcal H_\infty$ / $\mathcal H_2$ est un outil puissant et mature qui permet d’optimiser le contrôleur en prenant en compte plusieurs objectifs, automatiquement et de façon robuste aux incertitudes, afin de réduire les itérations entre le réglage du contrôleur et le processus de vérification et de validation (V&V). Du point de vue de l’ingénieur de contrôle, le processus de réglage consiste essentiellement à :
- Obtenir un modèle du système, incluant éventuellement des incertitudes paramétriques sous le formalisme LFT, par exemple en utilisant la SDTlib.
- Formuler des exigences de contrôle, sous forme de normes de transferts entre certaines entrées et sorties bien choisies, et écrire les filtres de pondération adéquats selon les spécifications. Par exemple, une exigence de rejet de perturbation peut être exprimée comme une borne sur la norme du transfert entre la perturbation et l’erreur de pointage, afin d’assurer une précision de pointage donnée.
- Utiliser la routine systune implémentée dans la Robust control toolbox de Matlab.
Références
[GA94] Pascal Gahinet and Pierre Apkarian. “A linear matrix inequality approach to H infinity control”. In: International Journal of Robust and Nonlinear Control 4 (1994), pp. 421–448.
[Apk04] Pierre Apkarian et al. “A spectral quadratic-SDP method with applications to fixed-order H2 and H infinity synthesis”. In: European Journal of Control 10.6 (2004), pp. 527–538.
[AN06a] Pierre Apkarian and Dominikus Noll. “Nonsmooth H infinity synthesis”. In: IEEE Transactions on Automatic Control 51.1 (2006), pp. 71–86.
[AN06b] Pierre Apkarian and Dominikus Noll. “Nonsmooth optimization for multidisk H infinity synthesis”. In: European Journal of Control 12.3 (2006), pp. 229–244.
[AN06c] Pierre Apkarian and Dominikus Noll. “The H infinity Control Problem is Solved”. In: Aerospace Lab 13 (2006), pp. 1–27.
[ADN15] Pierre Apkarian, Minh Ngoc Dao, and Dominikus Noll. “Parametric Robust Structured Control Design”. In: IEEE Transactions on Automatic Control 60.7 (2015), pp. 1857–1869. arXiv: 1405.4202.
