Le formalisme TITOP (Two-Input Two-Output Port) a été développé à l’ISAE-Supaero pour modéliser des structures flexibles au sein d’un formalisme multicorps [1].
Le modèle TITOP d’un corps flexible (un panneau solaire par exemple, ou bien une antenne, un bras robotique…) décrit sa dynamique de façon indépendante du reste du système. En assemblant des modèles TITOP, on peut donc construire le modèle d’une structure complexe tout en gardant des paramètres physiques pour chaque sous-structure.
La figure suivante représente une structure flexible quelconque notée $L_i$, connectée à une structure parent $L_{i-1}$ au point P, et à une structure enfant $L_{i+1}$ au point C.
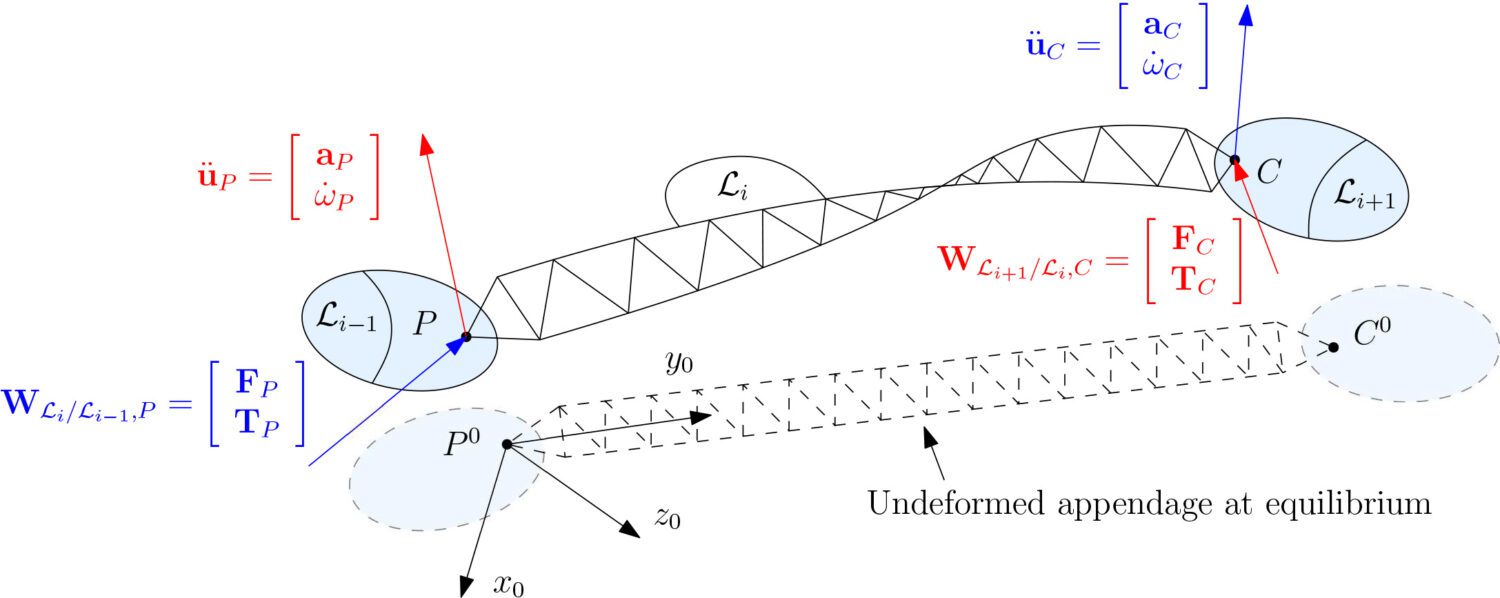
Le modèle TITOP de cette structure est le transfert 12×12 entre les entrées (en rouge) :
- $W_{L_{i+1}/L_i,P}$ le torseur contenant la force et le couple appliqué par $L_{i+1}$ sur $L_i$ au point C,
- $\ddot u_P$ les accélérations (translation et rotations) imposées à $L_i$ au point P,
Et les sorties (en bleu) :
- $\ddot u_C$ les accélérations résultantes au point C (avec les composantes rigides et flexibles),
- $W_{L_i/L_{i-1,P}}$ le torseur appliqué par $L_i$ à $L_{i-1}$ en réaction au point P.
Ici, le corps flexible est donc encastré en P – libre en C ; mais la SDTlib effectue les opérations d’inversion nécessaires pour obtenir toutes conditions au limites [2]. Par ailleurs, malgré la dénomination « TITOP », l’approche a été généralisée à tout nombre de points de connections (et pas seulement 2).
Le modèle TITOP est construit à partir des données mécaniques de la structure. Il peut ensuite être connecté à la structure, aussi bien pour des configurations simples (comme un panneau solaire encastré au corps central en un point) que complexes (chaînes cinématique ouverte représentant un bras robotique, assemblage de plaques en chaîne cinématique fermée pour modéliser un panneau solaire…). Il est compatible avec la représentation des incertitudes sous forme LFT (Linear Fractional Transformation) afin de produire un modèle entièrement paramétré.
Dans certains cas, le modèle de la structure ne peut pas être exprimé de façon indépendante du reste de la structure. C’est notamment le cas lorsqu’il dépend de conditions d’équilibre particulières, par exemple en présence de gravité (pour un ballon stratosphérique ou un lanceur) ou d’une force centrifuge (pour un satellite spinné). Pour exprimer le modèle dynaique du corps flexible, isolé de la structure et en conservant la représentation des incertitudes paramétriques sous forme LFT, il faut alors calculer les conditions d’équilibre comme proposé dans [3].
Dans la SDTlib, des modèles analytiques sont implémentés pour des formes simples (plaques et poutres), ainsi que des modèles à éléments finis pour des assemblages de plaques ; pour des structures plus complexes, il est également possible de renseigner directement les fréquences de résonance et les facteurs de participation modales, obtenus par tout autre software externe, ou bien de rentrer directement le fichier f06 fourni par Nastran. Le modèle TITOP est généré et peut être utilisé pour modéliser les éléments flexibles du satellite.
Références
[1] Alazard, D., Perez, J. A., Cumer, C., & Loquen, T. (2015). Two-input two-output port model for mechanical systems. In AIAA Guidance, Navigation, and Control Conference (p. 1778).
[2] Alazard, D., Finozzi, A., & Sanfedino, F. (2023). Port inversions of parametric Two-Input Two-Output Port models of flexible substructures. Multibody System Dynamics, 57(3-4), 365-387.
[3] Kassarian, E., Sanfedino, F., Alazard, D., Chevrier, C. A., & Montel, J. (2022). Linear Fractional Transformation modeling of multibody dynamics around parameter-dependent equilibrium. IEEE Transactions on Control Systems Technology.
