Contexte
Le terme « incertitude » fait référence aux écarts, nécessaires, entre le modèle mathématique d’un système physique et la réalité. De telles incertitudes peuvent dégrader la stabilité ou les performances du système, et motiver des considérations de robustesse dès la conception du contrôle. En particulier, on peut distinguer les incertitudes non structurées, qui traduisent toutes sortes de dynamiques négligées comme la dynamique haute fréquence ou les non-linéarités, des incertitudes structurées, ou paramétriques, désignant le fait que la valeur d’un paramètre n’est pas parfaitement connue, mais se situe dans un intervalle délimité autour d’une valeur nominale. Les incertitudes paramétriques sont courantes ; elles peuvent résulter, par exemple, d’erreurs de fabrication ou de mesure, de conditions de fonctionnement variables, de caractéristiques variables dans le temps ou de limitations inhérentes à la modélisation.
Représentation mathématique
Dans le SDTlib, et plus généralement dans le cadre du contrôle robuste linéaire, les incertitudes paramétriques (structurées) sont modélisées avec le formalisme des Transformations Fractionnaires Linéaires (LFT en anglais). La représentation d’état nominale s’écrit :
\begin{equation}
\left\lbrace \begin{array}{l}
\mathbf{\dot x} = \mathbf A \mathbf x + \mathbf B \mathbf u \\
\mathbf y = \mathbf C \mathbf x + \mathbf D \mathbf u
\end{array}
\right.
\end{equation}
Où $\mathbf x$ est le vecteur d’état, $\mathbf u$ est le vecteur d’entrée, $\mathbf y$ est le vecteur de sortie et les matrices A, B, C, D ont des dimensions appropriées. Dans la représentation de l’espace d’états incertains, ces matrices dépendent d’un ensemble de paramètres incertains $\delta_i$ :
\begin{equation}
\left\lbrace \begin{array}{l}
\mathbf{\dot x} = \mathbf A(\delta_i) \mathbf x + \mathbf B(\delta_i) \mathbf u \\
\mathbf y = \mathbf C(\delta_i) \mathbf x + \mathbf D(\delta_i) \mathbf u
\end{array}
\right.
\end{equation}
Le cadre LFT permet de réécrire cette représentation d’état sous une forme où les incertitudes sont isolées du modèle nominale :
\begin{equation}
\left\lbrace \begin{array}{l}
\mathbf{\dot x} = \mathbf A \mathbf x + \mathbf B_1 \mathbf u + \mathbf B_2 \mathbf w_\Delta\\
\mathbf y = \mathbf C_1 \mathbf x + \mathbf D_{11} \mathbf u + \mathbf D_{12} \mathbf w_\Delta \\
\mathbf z_\Delta = \mathbf C_2\mathbf x + \mathbf D_{21} \mathbf u + \mathbf D_{22} \mathbf w_\Delta \\
\mathbf w = \Delta \mathbf z \\
\end{array}
\right.
\end{equation}
Où la matrice inconnue, mais bornée, $\Delta = \mathrm{diag}(\delta_i \mathbf I_{n_i})$ (où $n_i$ est le nombre d’occurrences du paramètre $\delta_i$, et $\mathbf I_{n_i}$ est la matrice identité de taille $n_i$) est exprimée comme une rétro-action sur le modèle nominal. La figure suivante représente le schéma fonctionnel correspondant, où $\mathbf M(\mathrm s)$ est la matrice de transfert appropriée. Sans perte de généralité, étant donné que la normalisation peut être intégrée dans la matrice $\mathbf M(\mathrm s)$, on peut supposer que les $\delta_i$ vérifient $\mid \delta_i \mid < 1$.
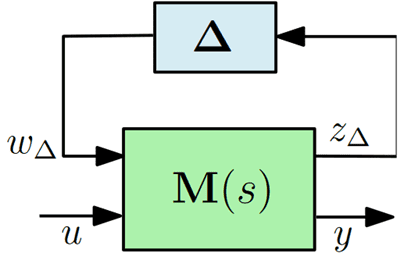
Exemple
Une masse m avec ±10% d’incertitude peut être représentée sous la forme :
\begin{equation}
m = m_0 (1+0.1\delta)
\end{equation}
où $m_0$ est la valeur nominale, et $\delta$ est un nombre réel inconnu tel que $\mid \delta \mid < 1$. Le schéma bloc correspondant est représenté sur la figure suivante.
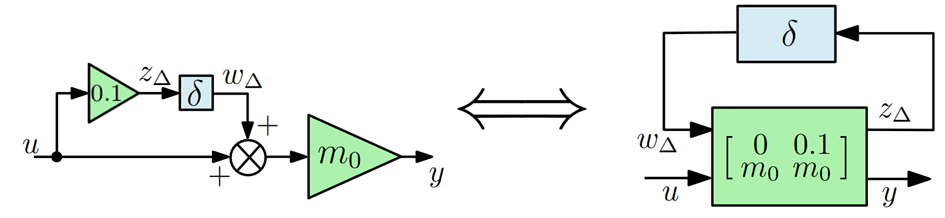
En pratique
Construire un modèle LFT d’un système avec des paramètres incertains consiste à trouver une représentation sous forme de schéma fonctionnel du système et à « isoler les deltas », comme dans l’exemple ci-dessus. En particulier, elle nécessite que les matrices $\mathbf A(\delta_i)$, $\mathbf B(\delta_i)$, $\mathbf C(\delta_i)$, $\mathbf D(\delta_i)$ soient des fonctions polynomiales ou rationnelles des incertitudes paramétriques $\delta_i$.
La forme LFT permet de représenter le système incertain avec un seul modèle continu au lieu d’une famille discrète de modèles à différents points de fonctionnement. Il permet à des outils d’analyse et de contrôle modernes tels que la mu-analyse ou le contrôle robuste H infini, de garantir une stabilité et des performances robustes face aux incertitudes paramétriques. Dans un satellite et dans la SDTlib, les incertitudes paramétriques peuvent être: la masse ou l’un des moment d’inertie d’un élément, les fréquences propres d’un panneau solaire, la position d’un point de connexion entre deux éléments…
Références
[ZDG96] Kemin Zhou, John C Doyle, and Keith Glover. Robust and Optimal Control. Englewood Cliffs: Prentice hall, 1996.
